Optimised Latin Hypercube Sampling Plan

Create an optimised Latin Hypercube Sampling Plan using a genetic based optimisation algorithm. The objective function is the inverse of the Audze-Eglais function defined as

\[\text{max } U = \text{max} \frac{1}{\sum_{p=1}^P \sum_{q=p+1}^P \frac{1}{L^2_{pq}}}\]

Note

This package maximises the inverse of the Audze-Eglais objective function.

where $L_{pq}$ is the Euclidean norm. It is also possible to choose powers other than 2 by using the ae_power optional parameter.

There is also an option to use a periodic version of the Audze-Eglais which reduces clustering along the boundaries of the sampling plan. The implementation follows the paper:

Jan Eliáš, Miroslav Vořechovský, Modification of the Audze–Eglājs criterion to achieve a uniform distribution of sampling points, Advances in Engineering Software, Volume 100, 2016, Pages 82-96, ISSN 0965-9978, () https://doi.org/10.1016/j.advengsoft.2016.07.004.

Function

LatinHypercubeSampling.LHCoptim — Method

function LHCoptim(n::Int,d::Int,gens;   rng::U=Random.GLOBAL_RNG,
                                        popsize::Int=100,
                                        ntour::Int=2,
                                        ptour=0.8,
                                        dims::Array{T,1}=[Continuous() for i in 1:d],
                                        interSampleWeight::Float64=1.0,
                                        periodic_ae::Bool=false,
                                        ae_power::Union{Int,Float64}=2) where T <: LHCDimension where U <: AbstractRNG

Produce an optimized Latin Hyper Cube with d dimensions and n sample points. Optimization is run for gens generations. Returns a tuple of the sample plan and the optimization fitness history.

source

Where gens is the number of generations to run the optimisation for. The population size, number of samples selected for tournament, as well as the probability for tournament selection in the genetic algorithm, can be accessed with the optional arguments popsize=100, ntour=2 and ptour=0.8. These are manually tuned defaults and may not be optimal depending on the number of dimensions and the size of the plan.

The RNG can be specified or else the global RNG will be used.

Multithreading can be used by starting Julia with multiple threads and specifying threading=true.

Note

Specifying a rng does not yield the same result each time when running the plan threaded.

The optimisation of a sampling plan is started from a random plan which is also an exported function.

LatinHypercubeSampling.randomLHC — Method

function randomLHC(n::Int, d::Int)

Generate a random Latin Hypercube with d dimensions and n sample points.

source

Example

The LHCoptim function run for many generations to create an optimised 120 point plan in 2 dimensions. Both the plan and the fitness of the sampling plan are exported.

julia> plan, fitness = LHCoptim(120,2,gens)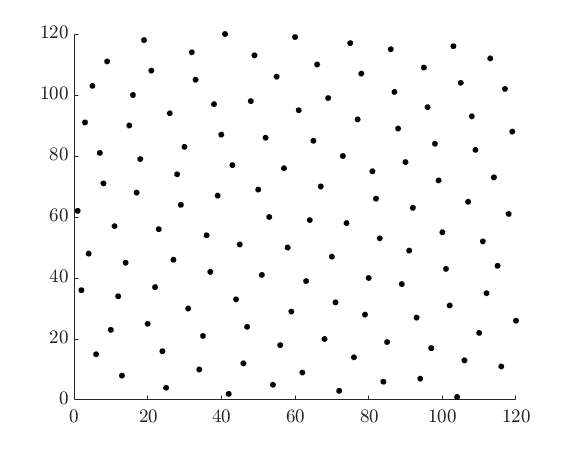

If only the plan is required, the fitness can be omitted using

julia> plan, _ = LHCoptim(120,2,gens)

The results can be scaled to a suitable range with the exported function scaleLHC.

julia> plan, _ = LHCoptim(100,2,1000)
julia> scaled_plan = scaleLHC(plan,[(-5.0,5.0),(-5.0,5.0)])

which can then be used to sample a function as

julia> rosenbrock_2D(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2
julia> mapslices(rosenbrock_2D,scaled_plan; dims=2)